Cours gestion budgétaire => Gestion budgétaire de la production
Chapitre 2 : Gestion budgétaire de la production
La budgétisation de la production est la représentation globale chiffrée de l’activité productive annuelle. Mais ce n’est que l’aboutissement final de toute la procédure de gestion de la production.
– Les techniques de gestion de production :
Il s’agit de répondre aux questions suivantes :
- Combien faut-il produire pour répondre à la demande en tenant compte des contraintes techniques de fabrication ? les méthodes de programmation linéaire permettent de résoudre ce problème.
- Combien faut-il commander et stocker de matières premières pour satisfaire la demande prévue ? la réponse est apportée par le calcul des besoins en composa
- Comment et combien faut-il charger les ateliers, les machines, les capacités humaines pour que la production corresponde aux besoins ? les méthodes de chargement gèrent les goulots d’étrangleme
1-1 La programmation linéaire :
Cette technique a pour objectif d’assurer le plein emploi des capacités productives en fonction des objectifs de vente et de choisir une combinaison productive de produits qui maximise la rentabilité.
- programme de production pour le plein emploi :
L’illustration de cet outil sera envisagé dans le cadre de l’exemple suivant :
Soit une entreprise de construction mécanique qui produit trois types de roulements R1, R2 et R3. Les trois types de roulements passent successivement dans trois ateliers. Leurs temps de passage en heures et par atelier sont les suivants :
| Produits Ateliers | R1 | R2 | R3 | Capacité des ateliers |
| A1 | 4 | 2 | 1 | 2600 heures |
| A2 | 3 | 3 | 2 | 2500 heures |
| A3 | 2 | 5 | 3 | 3000 heures |
Pour des impératifs commerciaux, la production des roulements R3 est fixée à 200 unités.
Existe-t-il un programme de production qui assure le plein emploi des capacités ?
Les contraintes peuvent être mises en équation, en prenant pour acquis la vente et la production de 200 R3. Le choix se situe entre R1 et R2.
Atelier A1 : 4R1+2R2+R3 £ 2600 4R1+2R2 £ 2600-(200 R3*1) soit 2400.
Atelier A2 : 3R1+3R2 £ 2500 -(200 R3 * 2) soit 2100.
Atelier A3 : 2R1+5R2 £ 3000 -(200 R3 * 3) soit 2400.
Démarche générale :
Chaque contrainte partage le plan en trois zones :
- La droite qui représente toutes les combinaisons de produits qui saturent la contrainte.
- La zone en dessous de la droite où les combinaisons respectent la contrainte mais n’assurent pas le plein emploi de ses capacité
- La partie supérieure du plan où les combinaisons sont inacceptable
Pour assurer le plein emploi simultané des contraintes productives, il faut rechercher les combinaisons productives qui saturent toutes les contraintes concernées.
Suite de l’exemple :
L’ensemble des contraintes définit un polygone de combinaisons acceptables ABCDE . Aucun point de ce domaine ne permet de saturer toutes les contraintes de production. Seules les points B et C assurent le plein emploi de deux des trois contraintes de production.
Solution B : intersection de l’atelier A2 et A3. Il suffit de résoudre le système d’équation suivant pour obtenir la combinaison des produits.
3R1 + 3R2 = 2100
2R1 + 5R2 = 2400 on obtient 367 R1 et 333 R2.
L’atelier A1 est en sous-emploi de 2400-(367R1*4)-(333R2*2) = 266 heures.
Solution C : intersection de l’atelier A1 et A2. Elle donne 500 R1 et 200 R2. L’atelier A3 est en chômage pour 2400-(500R1*2)-(200R2*5) = 400 heures.
A cette étape du raisonnement, le choix doit se faire entre le coût relatif du chômage de chaque atelier. L’entreprise peut aussi chercher les solutions qui permettent d’augmenter les capacités des ateliers (heures supplémentaires, réorganisation du travail…etc).
Dans les cas envisagés précédemment, c’est l’atelier A2 qui limitait la production et obligeait au sous-emploi des autres ateliers : on qualifie cette situation de goulot d’étranglement.
Suite de l’exemple :
L’entreprise décide d’affecter des capacités supplémentaires pour obtenir le plein emploi de ses trois ateliers. Dans ce cas, elle choisit la combinaison M (450 R1 et 300 R2). L’atelier A2 devrait disposer d’une capacité de : (450R1*3)+(300R2*3) = 2250 heures. Si l’entreprise veut choisir cette solution, elle doit affecter une capacité supplémentaire de 150 heures à l’atelier A2 (2250-2100).
- La solution optimale en terme de rentabilité :
Les choix de l’entreprise ne peuvent s’effectuer sans référence aux coûts des ateliers ni à la rentabilité des différents produits. Pour illustration, reprenons l’exemple précédent.
Supposons que les produits R1, R2 et R3 dégagent respectivement une marge sur coûts variables de 160,140 et 50 dh.
La solution optimale est celle qui maximise la MCV globale, càd Max dh =160R1+140R2.
La fonction ainsi définie est appelée fonction économique du programme. Elle peut s’écrire aussi : R2 = -1,15 R1 + Max dh. C’est une fonction de la forme ax+b et Max dh est une constante qu’il faut maximiser. Cela revient à chercher la droite de pente égale à -1,15 et dont l’ordonnée à l’origine est maximum. Il existe une solution graphique :
Démarche générale :
La fonction économique (F) doit être représentée au point E. Il existe toute une famille de droites parallèles à F et qui possèdent des ordonnées à l’origine de plus en plus élevés dès que l’on se déplace vers le haut du graphique. Le déplacement d’une droite parallèle à la droite tracée permet de déterminer le point d’intersection entre le polygone des solutions acceptables et la fonction économique : ce point est celui de la solution optimale. Ici c’est le point C représentant une combinaison de 500R1 et 200R2.
NB : La solution graphique n’est valable que dans le cas de deux produits. Dès que le nombre de produits s’accroît, il faut recourir aux techniques du simplexe.
1-2 Calcul des besoins en composants :
La planification des besoins en composants PBC correspond à la gestion des stocks de matières premières nécessaires à la production. Ce calcul s’insère dans un système plus large de gestion de production : le MRP (Management Ressources Planning).
Le MRP est un système de pilotage par l’amont du processus de production, il se compose de plusieurs étapes :
- Le plan industriel et commercial : Il est élaboré par familles de produits et représente un calendrier des ventes et du niveau des stocks sur une période variable suivant le cycle de fabrica Il s’appuie sur la relation suivante :
Production prévisionnelle = ventes prévis. + niveau de stock désiré – niveau de stock actuel.
- Le programme directeur de production : qui rassemble l’ensemble des demandes sur la production et établit un échéancier des productions à effectuer. Son horizon est la semaine ou le jour. Il doit être compatible avec les capacités des usines et les prévisions commerciale
- Le calcul des besoins : il précise pour chaque élément les besoins en quantité de tous les articles achetés ou réalisés par l’entreprise ainsi que les dates de fabrication ou d’approvisionneme
- Le calcul des charges : analyse les postes de travail en capacité et gère les flux entrants et sortants dans chaque atelier. Il permet aux gestionnaires de repérer les goulots d’étrangleme
- Les contrôles d’exécution ordonnancent la charge de travail entre les postes une fois les problèmes de sous ou sur capacité réglé Il planifie les priorités des ordres de fabrication.
a- Le principe du calcul des besoins en composants :
Chaque produit est composé d’ensembles, de sous-ensembles et de pièces. Ce sont ces composants de base que les services de production doivent usiner. Le programme prévisionnel des ventes exprimées en nombre de produits doit être transcrit en éléments de base dont la charge de travail est à répartir dans le temps et l’espace.
La fabrication d’un produit est composée de phases d’usinage et d’assemblage. Chaque étape de fabrication est caractérisée par : un élément, une opération qui s’effectue sur l’élément et une durée pour réaliser cette opération. Cet ensemble forme une nomenclature qui permet de définir des besoins dépendants et des besoins indépendants.
- Les besoins indépendants sont constitués de pièces ou produits achetés en l’état à l’extérieur. La prévision de tels besoins, repose sur une bonne prévision des vente
- Les besoins dépendants sont formés des sous-ensembles nécessaires aux produits f
Leur prévision repose sur des calculs fiables.
1-3 Les méthodes de chargement et les goulots d’étranglement :
La notion de goulot d’étranglement est liée au concept de chargement des ateliers et à un manque de capacité pour satisfaire les besoins de fabrication répertoriés.
- Tableau de chargement des ateliers :
Exemple : dans deux ateliers A1 et A2, trois produits X, Y et Z doivent être usinés. Le temps (en heures) nécessaire à l’usinage de chacun des produits est le suivant :
| Produits Ateliers | X | Y | Z |
| Atelier A1 Atelier A2 | 1 1 | 3 2 | 2 5 |
Les temps de chargement des différents postes de travail sont de 2000 heures par an dans l’atelier A1 et de 2100 heures dans l’atelier A2. Il faut compter 10% pour les temps de réglage et de changement d’outils pendant lesquels les machines ne sont pas en état de marche.
Le nombre maximum de postes utilisables est de 20 pour A1 et 18 pour A2.
Le budget des ventes prévoit 7000X, 6000Y et 4000Z. Les lots de fabrication doivent respecter la proportion des ventes (hypothèse de production simultanée).
Établir un programme de chargement qui permet les ventes en quantités maximales.
Démarche générale :
Il faut calculer les capacités nécessaires à la production maximale, calculer les capacités disponibles et ajuster le désirable et le possible.
Suite de l’exemple : tableau provisoire des temps de chargement.
| Intitulé | Atelier 1 | Atelier 2 |
| Calcul des capacités nécessaires | 7000 | 7000 |
| Pdt X (7000 * temps de fabrication) | ||
| Pdt Y (6000 * temps de fabrication) | 18000 | 12000 |
| Pdt Z (4000 * temps de fabrication) | 8000 | 20000 |
| Capacités nécessaires (a) | 33000 | 39000 |
| Calcul des capacités disponibles | 1800 | 1890 |
| Temps de marche par poste de travail | ||
| (temps de chargement * 0,90) | ||
| Nombre de poste par atelier | *20 | *18 |
| Capacités disponibles (b) | 36000 | 34020 |
| Excédent de capacité (b) – (a) Manque de capacité (a) – (b) | 3000 | 4980 |
| Taux de chargement (a) / (b) | 0,916 | 1,146 |
L’atelier A2 a un taux de chargement supérieur à 1 ce qui n’est pas réaliste. Cet atelier présente un manque de capacité de 4980 heures: c’est un goulot d’étranglement.
Ajustement :
La contrainte de fabrication simultanée et dans la proportion donnée (7X pour 6Y et 4Z) définit une combinaison productive qui consomme lors de son passage dans l’atelier A2 : (7X*1) + (6Y*2) + (4Z*5) = 39 heures.
Dans les capacités disponibles de l’atelier A2, on peut avoir 34020 / 39 = 872 combinaisons de base et donc une fabrication de :
7X*872 soit 6104X arrondie à 6100 unités, 6Y*872 soit 5232Y arrondie à 5230 unités, 4Z*872 soit 3488Z arrondie à 3480 unités.
On peut alors présenter le tableau de chargement définitif :
| Intitulés | Atelier 1 | Atelier 2 |
| Calcul des capacités nécessaires | 6100 | 6100 |
| Produit X (6100 unités) | ||
| Produit Y (5230 unités) | 15690 | 10460 |
| Produit Z (3480 unités) | 6960 | 17400 |
| 28750 | 33960 | |
| Capacités disponibles | 36000 | 34020 |
| Excédent de capacité | 7250 heures | 60 heures |
| Taux de chargement | 0,80 | 1 |
Avec ce programme, les taux de chargement sont tous inférieurs ou égaux à 1 mais l’atelier A1 est en chômage pour 7250 heures.
Goulot d’étranglement et choix des produits :
Les programmes précédents ont été obtenus sans référence aux coûts et aux marges générées par produits. La gestion optimale d’un goulot d’étranglement ne peut s’effectuer hors des éléments de prix.
Suite de l’exemple : le contrôleur de gestion vous fournit les renseignements suivants :
| X | Y | Z | |
| Marge sur coût variable par produit | 150 dh | 320 dh | 400 dh |
Il vous demande d’établir le programme de production qui génère la plus grande marge totale.
Démarche générale :
Il s’agit de saturer les capacités de l’atelier qui constitue le goulot d’étranglement en produisant des quantités différentes de X, Y et Z. Il n’y a plus de production simultanée.
NB : l’élément rare n’est pas un des produits mais l’unité de facteur du goulot (ici, l’heure de marche des machines de l’atelier). Il faut donc utiliser ces heures à produire ce qui rapporte le plus, non pas en terme de produits mais en terme de marge par unité de facteur du goulot. Suite de l’exemple :
Calcul de marge par heures de passage et par produit dans l’atelier A2 :
| X | Y | Z | |
| Marge sur coût variable par produit | 150 | 320 | 400 |
| Temps de passage par produit (en heures) | 1 | 2 | 5 |
| Marge sur coût variable horaire | 150 | 160 | 80 |
| Ordre de fabrication | 2 | 1 | 3 |
Le programme de production s’établit ainsi :
| Quantités de produits | Temps nécessaire | Temps disponible | Marge sur coût variable |
| 6000 Y | 12000 h | 34020 | 1 920 000 |
| 22020 | |||
| 7000 X | 7000 h | 15020 | 1 050 000 |
| 3004 Z | 15020 h | 0 | 1 201 600 |
| Marge sur coût variable totale | 4 171 600 | ||
Ce programme assure une utilisation optimale des heures de l’atelier A2 et est compatible avec les capacités de l’atelier A1. Il est facile de vérifier que le nombre d’heures de fonctionnement dans cette hypothèse s’élève à 31008 heures pour A1 et donne un taux de chargement supérieur ( 0,86 au lieu de 0,80 précédemment).
II la budgétisation de la production :
Après avoir défini les variables d’action, il faut ventiler le programme de production en autant de budgets que nécessaire. Ce travail de budgétisation est réalisé en collaboration avec les services techniques productifs et le contrôle de gestion.
2.1 Partage des tâches entre la production et le contrôle de gestion :
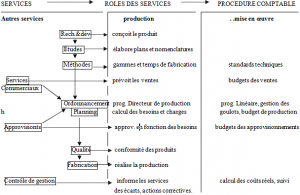
2.2 valorisation du programme de production :
Pour présenter un plan de production valorisé, l’entreprise utilise les coûts standards des produits (voir les coûts préétablis). Ce chiffrage représente l’objectif des services productifs. Dans ce chiffrage les charges directes et indirectes de production sont éclatés dans le temps (le mois) et dans l’espace en fonction de la répartition géographique de la production et des responsabilités.
Ces services doivent proposer un plan d’action permettant de respecter, dans les conditions du budget, leurs obligations en matière de production. Ce plan envisage les variables suivantes :
- le taux de perte de matières premières,
- le taux de productivité de la main d’œuvre,
- les effectifs,
- la sous-traitance en volume (éventuellement),
- l’entretien préventif en taux d’heures perdues, etc.
III Calcul des écart sur coût de production :
I- définitions :
Un coût prévisionnel est un coût calculé à priori, on distingue plusieurs types de coûts selon la méthode de calcul :
- le coût préétabli :
C’est un coût calculé à partir de l’analyse du passé, par exemple le coût de la période précédente ou le coût moyen calculé sur plusieurs périodes passées.
Exemple : le coût d’achat constaté pour la matière M pour le premier trimestre 2002 est :
- janvier 15 dh / unité
- février 17 dh / unité
- mars 16 dh / unité
Le coût préétabli pour M en avril sera de 15+17+16/3 =16 dh/ unité.
- le coût budgété :
C’est un coût prévisionnel calculé à partir des budgets de fonctionnement des différents centres de l’entreprise.
- le coût standard :
Le standard est une quantité ou une valeur maintenue constante au cours d’une période. Le coût standard est alors le résultat d’une étude technique et économique des conditions de production effectuée par le bureau d’études et de méthodes de l’entreprise.
Exemple :
Si on envisage le cas d’un produit connu comme une chemise, elle nécessite du tissu, des boutons, du fil et trois opérations; la coupe, le montage et la finition.
L’analyse définira pour chaque élément (matière ou opération) 2 standards :
- un standard de quantité qui dépend de la taille du vêtement, du modèle envisagé
- un standard de coût qui varie avec la qualité du tissu, la qualification da la main d’œuvre…etc.
Ainsi, on peut élaborer une fiche de coût standard pour un produit comme suit :
Fiche de coût standard
Prix standard M1ère * quantité standard M1ère
+ Taux standard de MOD * Temps standard MOD
+ Taux standard des UO * nombre standard des UO
= coût standard du produit fabriqué
2. le pilotage par les écarts :
L’objectif est ici de confronter les normes préétablies concernant la production, avec la réalisation afin de calculer et d’analyser les écarts pour une bonne maîtrise des coûts.
- Le calcul de l’écart global sur charges:
EG= charges réelles – charges prévues pour la production réelle
= (Qr * Pr) – (Qp * Pp)
Cet écart se calcule pour les charges directes et indirectes:
Charges directes matières premières écart/M1
main d’œuvre directe écart/MOD
Charges indirectes centre d’analyse A écart/A
Centre d’analyse B écart/B
- l’analyse de l’écart sur charges directes :
L’écart global sur CD = coût réel – coût préétabli
Un coût s’obtient en multipliant la quantité par un coût unitaire, la décomposition de l’écart globale donne :
EG = (Qr*Pr) – (Qp*Pp) avec Qp : quantité préétablie pour la production réelle. Cet écart peut s’analyser en un écart sur quantité et un écart sur prix.
Exemple :
L’entreprise SIM vous communique les prévisions pour la fabrication d’un produit fini A :
- matières premières : 1 200 kg à 11,8 DH/kg
- MOD : 1 000 heures à 50 DH/h
La production normale (prévue, standard) est de 2 000 produits finis A. A la fin du mois, les données réelles sont :
- production réelle : 2 200 produits
- consommation des matières premières : 11 000 kg à 13 200 DH
- le temps de MOD est de 33 minutes par produit à 52 DH l’heure
Calculer l’écart global sur M1ère et MOD
Décomposer cet écart en écart sur quantité et écart sur prix
- Analyse de l’écart sur charges indirectes :
a- Définition :
C’est la différence entre le coût réel du fonctionnement du centre et le coût qui aurait dû être prévu pour un niveau de production correspondant à la production réelle. Cet écart peut s’expliquer par :
- une différence par rapport au budget de fonctionnement du centre
- une différence du niveau d’activité
- une différence sur la qualité du travail
L’écart global sur charges indirectes se décompose donc en :
- écart sur budget
- écart sur activité (écart d’imputation rationnelle)
- écart sur rendement
b- analyse de l’écart :
notion de budget flexible :
Le budget flexible représente le coût de fonctionnement du centre pour différents niveaux d’activité.
Exemple :
Le budget de l’atelier montage de l’entreprise « X » est le suivant :
Activité normale

- Coût unitaire standard
L’écart sur budget (ou écart sur coût variable) :
E/B = coût réel – [ (CUVS * Ar) + CFt ]
Exemple : l’atelier montage de l’entreprise « X » a effectué une activité réelle de 900 heures évaluées à 34 000 DH.
E/B = 34 000 – [ (20 * 900) + 12 000]
= + 4 000 (écart défavorable)
Cet écart signifie que le fonctionnement de l’atelier a coûté 34 000 DH pour 900 heures au lieu de 30 000 DH prévus par le budget à ce niveau.
L’écart sur activité :
C’est la différence entre le budget prévu pour l’activité réelle et le coût d’imputation rationnelle qui lui correspond.
E/A = coût budgété – coût d’imputation rationnelle
= [(CUVS * Ar) + CFt] – [CUS * Ar]
Exemple : entreprise « X » E/A = 30 000 – (32 * 900)
= + 1 200 (défavorable)
L’écart sur rendement :
C’est la différence entre le coût de la production réelle et la production évaluée au coût préétabli.
E/R = (CUS * Ar) – (CUS * Ap)
Ap : activité qu’il aurait fallu prévoir pour obtenir la production réelle.
Ap = production réelle * rendement standard
Ar = production réelle * rendement réel Exemple entreprise « X »
E/R = (32 * 900) – (32 * 950) = – 1 600 (favorable)
Ap = (1000/100) * 9
 Cours et exercices
Cours et exercices